Data Structures - Linear List in Python
from random import randint
import sys
import numpy as np
import time
import pandas as pd
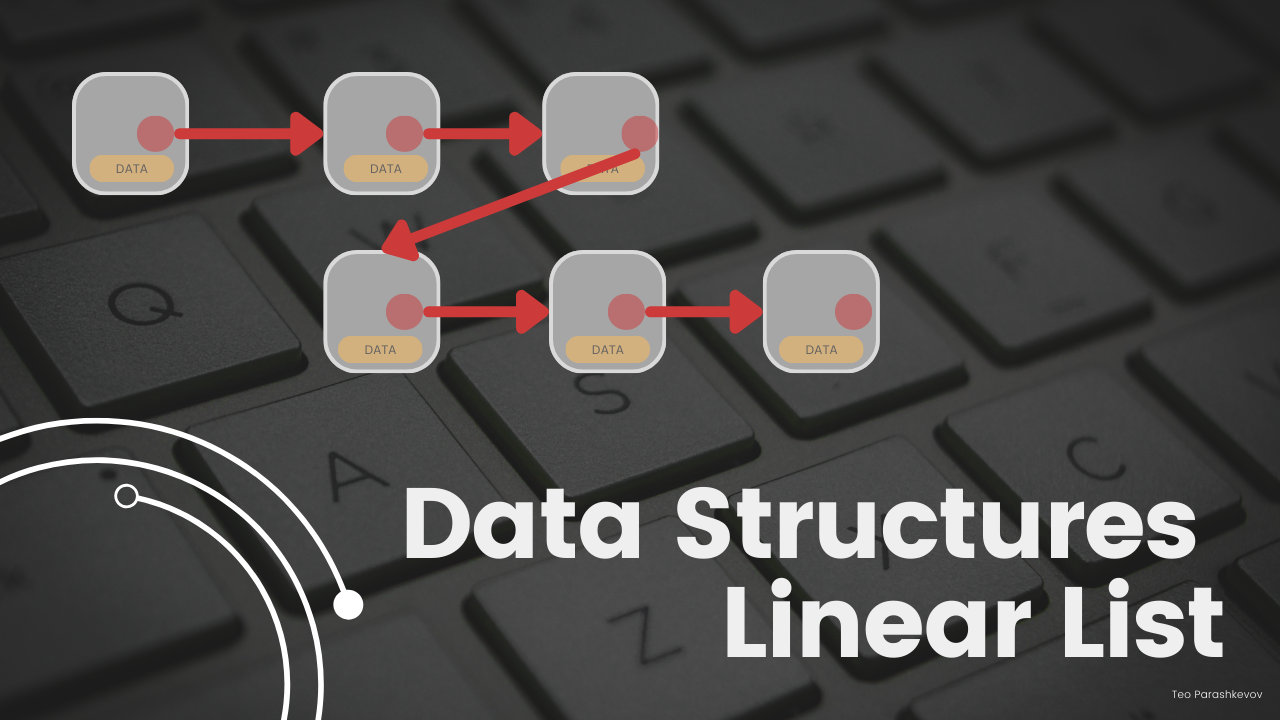
Linear List
Definition
A Linear List can be defined as a data structure that stores elements in a sequential manner, where each element is linked to its previous and next elements. The elements in a linear list are accessed in an ordered way, typically from the first element to the last, forming a linear relationship. This type of list allows for efficient element insertion and deletion operations at the beginning or end of the list, but less efficient operations for accessing or modifying elements in the middle.
Usages
The usage of a Linear List as a data structure encompasses various applications due to its sequential organization. Some notable usages of a Linear List include:
- Data storage and retrieval : Linear lists provide a straightforward way to store and retrieve data in an ordered manner. For example, a list of student records or sales transactions can be efficiently managed using a linear list.
- Queue implementation : A linear list can be used to implement a queue data structure, where elements are added at the end and removed from the beginning. This is particularly useful in scenarios requiring First-In-First-Out (FIFO) processing, such as job scheduling or message queuing.
- Stack implementation : A linear list can also be utilized to implement a stack data structure, where elements are added and removed from the same end. Stacks are commonly used in algorithmic problems, expression evaluation, and recursive function execution.
- Dynamic memory allocation : Linear lists, particularly linked lists, provide an effective way to dynamically allocate memory for elements during runtime. This allows for efficient management of memory resources, especially when the number of elements is unknown or changes frequently.
- Iterative processing : Linear lists enable iterative processing of data, as they can be traversed sequentially from one element to another. This makes them well-suited for algorithms that require sequential access, such as searching, sorting, and filtering operations.
These usages highlight the versatility and practicality of a Linear List as a data structure, making it a fundamental building block in many software systems and applications.
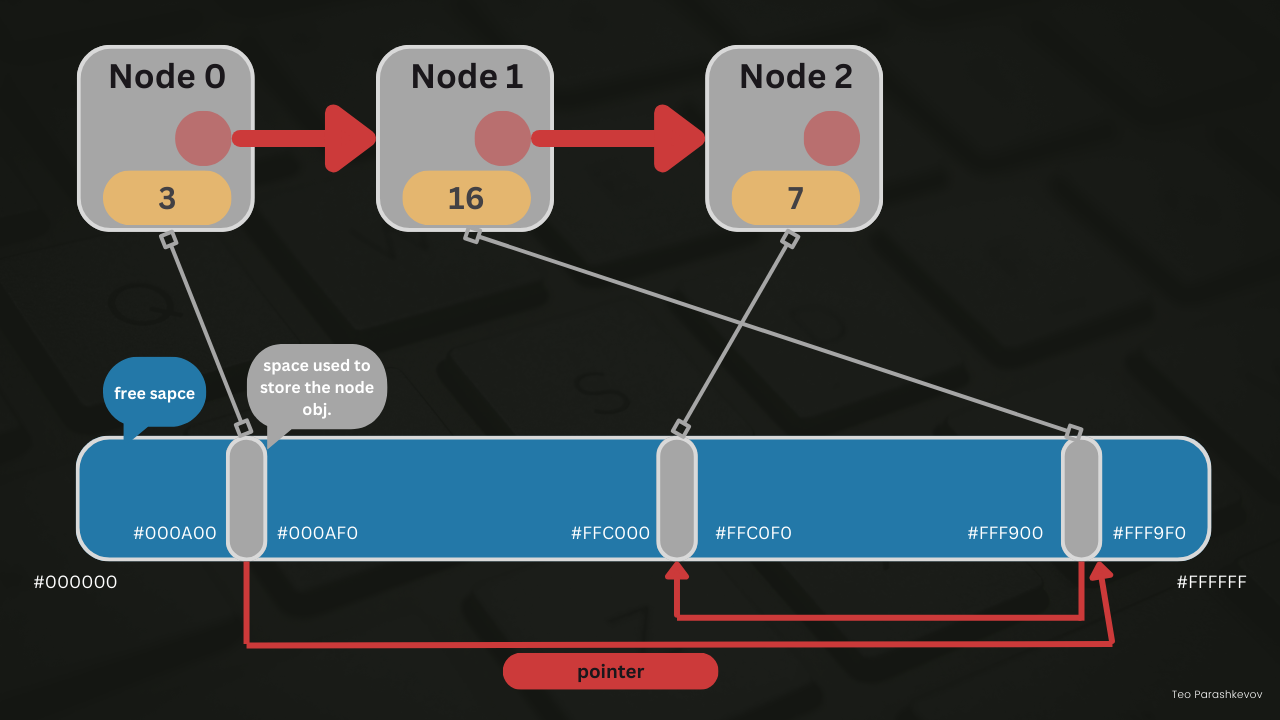
Sequential List (Array/List in Python)
Definition
A Sequential List is a type of data structure that utilizes an array as the means of storage. It is characterized by a contiguous block of memory where elements are stored in a sequential order. Each element in the sequential list can be directly accessed using an index, allowing for efficient random access.
In a sequential list, the array size is usually fixed at the time of creation, meaning that the number of elements in the list cannot exceed the allocated capacity. If the list needs to accommodate more elements, it may require resizing the underlying array, which can be an expensive operation.
The sequential list provides efficient access, insertion, and deletion operations at both ends of the list, but modifying or rearranging elements in the middle may involve shifting or moving a large number of elements, resulting in lower efficiency.
Overall, the sequential list is an important data structure that offers predictable memory usage and fast access times, making it suitable for scenarios where random access is frequently required and the number of elements remains relatively stable.
ACN (Average comparing number)
\[\begin{aligned} ACN = \sum_{i=1}^n p_{i}c_{i} \end{aligned}\]where $p_{i}$ is the probability and $c_{i}$ is the cost
AMN (Average moving number)
When Inserting \(\begin{aligned} AMN_{insert} &= \frac{1}{n+1} \sum_{i=1}^n (n-i) \\ &= \frac{1}{n+1} (n+\dots+1+0) \\ &= \frac{1}{n+1} \frac{n(n+1)}{2} \\ &= \frac{n}{2} \end{aligned}\)
When Deleting \(\begin{aligned} AMN_{delete} &= \frac{1}{n} \sum_{i=1}^n (n-i) \\ &= \frac{1}{n}((n-1)+\dots+1+0) \\ &= \frac{1}{n}\frac{(n-1)n}{2} \\ &= \frac{n-1}{2} \end{aligned}\)
Advantages of sequential lists (arrays):
- Constant-time access : Elements can be accessed in constant time using their index, making retrieval efficient.
- Efficient memory access : Sequential lists store elements contiguously in memory, allowing for efficient traversal and cache utilization.
- Simple implementation : The structure of sequential lists is straightforward, making them easy to understand and implement.
- Random access : Elements can be accessed randomly, allowing for quick retrieval of specific elements.
Disadvantages of sequential lists (arrays):
- Fixed size : Arrays have a fixed size determined during their creation, which cannot be changed dynamically. This can limit flexibility when the number of elements needs to grow or shrink.
- Memory overhead : Sequential lists allocate memory for a fixed number of elements, regardless of the actual number of elements stored. Therefore, if the array has few elements, there may be wasted memory.
- Costly resizing : If the size needs to be changed, resizing an array requires creating a new array and copying the elements, which can be time-consuming and resource-intensive.
- Insertion and deletion : Inserting or deleting elements in the middle of an array requires shifting subsequent elements, resulting in an inefficient operation.
- Homogeneous storage : Arrays can only store elements of the same type, as they are homogeneous. This can limit their usage in scenarios requiring different data types.
Advantages of sequential lists:
- Constant-time access
- Efficient memory access
- Simple implementation
- Random access
Disadvantages of sequential lists:
- Fixed size
- Memory overhead
- Costly resizing
- Inefficient insertion and deletion
- Homogeneous storage
class SequentialList(list):
pass
def create_sequential_list(size):
tmp_sq_list = SequentialList()
for i in range(size):
tmp_sq_list.append(randint(1, 100))
return tmp_sq_list
sequential_list = create_sequential_list(10)
print(sequential_list)
# Because Python List does not store elements equentially, here you cannot see a real example of a sequential list.
# In theory, the address of the first element is the starting point of the array - array[0] is located @ FFF123456.
# Each element is of the same type, which implies that each element is of the same size. If the size of the element is 4 Bytes,
# this means that accessing the 3rd element (i.e. index 2) will be located at:
# [Address of element 0] + [index of element]*[size of element]
# FFF123456 + 2*4
# FFF123456 + 8 = FFF12345E
#for idx, element in enumerate(sequential_list):
# id_current_elmnt = id(element)
# id_next_elmnt = id(sequential_list[idx + 1]) if idx < len(sequential_list) - 1 else 0
#
# print(f'Value [{element}] \t Address: [{id_current_elmnt}] \t Displacement [{id_next_elmnt - id_current_elmnt}]')
[15, 5, 71, 82, 4, 38, 83, 39, 26, 93]
Linked List
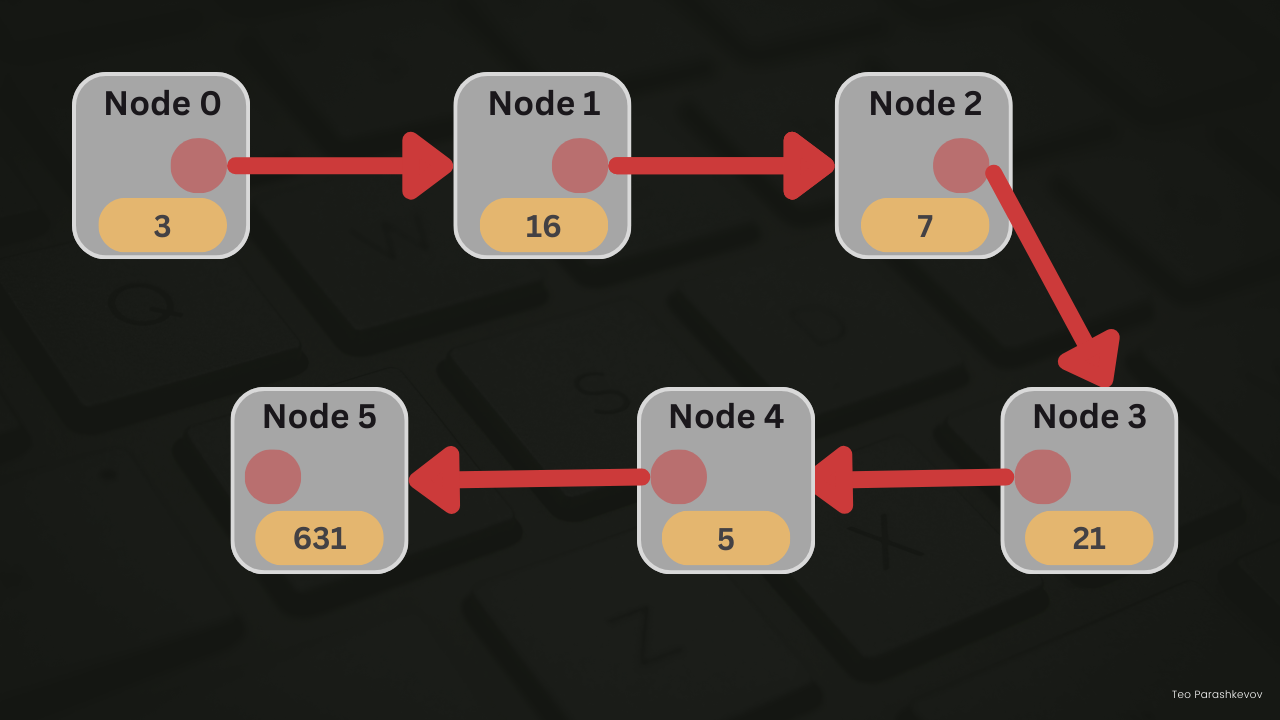
Definition
A Linked List can be defined as a subset of a linear list that consists of nodes, where each node holds a value and a pointer to the next node in the sequence. Unlike other linear list structures, such as arrays, a linked list does not require contiguous memory allocation. Instead, each node in the linked list is dynamically allocated and connected through pointers, enabling flexibility in element insertion, deletion, and rearrangement operations. This allows for efficient manipulation of elements in the middle of the list, at the cost of slower random access compared to arrays.
Advantages of linked lists:
- Dynamic size : Linked lists can dynamically grow and shrink based on the number of elements, providing flexibility.
- Efficient insertion and deletion : Insertion or deletion of elements in a linked list can be efficient, as it involves updating only a few pointers, rather than shifting elements.
- Memory efficiency : Linked lists can utilize memory efficiently by allocating memory chunk by chunk as elements are added, rather than requiring a fixed-size block like arrays.
- Easy to modify : Linked lists can be easily modified by changing the links between nodes, making them suitable for dynamic data structures.
- Supports different data types : Unlike arrays, linked lists can store elements of different data types, allowing for more flexibility.
Disadvantages of linked lists:
- Slow access time : Accessing elements in a linked list is slower compared to arrays because each element needs to be traversed from the beginning to reach a specific position.
- Extra memory overhead : Linked lists require additional memory to store the links connecting the nodes, which can result in inefficiency when dealing with small amounts of data.
- Sequential access only : Linked lists are designed for sequential access, making random access or efficient searching time-consuming.
- Not cache-friendly : Due to the scattered nature of linked list nodes in memory, they may not benefit from the cache locality, resulting in slower overall performance.
- More complex implementation : The implementation of linked lists can be more complex compared to arrays, involving dynamic memory allocation and maintaining proper links between nodes.
Advantages of linked lists:
- Dynamic size
- Efficient insertion and deletion
- Memory efficiency
- Easy to modify
- Supports different data types
Disadvantages of linked lists:
- Slow access time
- Extra memory overhead
- Sequential access only
- Not cache-friendly
- More complex implementation
Example (Linked List)
class Node:
def __init__(self, data):
self.data = data
self.next_node = None
def __next__(self):
return self.next_node
def __str__(self):
return '[' + str(self.data) + ']'
def iterate_print_data(self):
tmp_node = self
while tmp_node is not None:
if tmp_node.next_node is not None:
print(tmp_node, end=' -> ')
else:
print(tmp_node)
tmp_node = next(tmp_node)
def iterate_print_address(self):
tmp_node = self
while tmp_node is not None:
if tmp_node.next_node is not None:
print('[' + str(id(tmp_node)) + ']', end=' -> ')
else:
print('[' + str(id(tmp_node)) + ']')
tmp_node = next(tmp_node)
def create_linked_list(size):
head = Node('Head')
tail = Node('Tail')
last_node = None
for i in range(size):
created_node = Node(randint(1, 100))
if i == 0:
# Set Head
head.next_node = created_node
else:
last_node.next_node = created_node
last_node = created_node
# set Tail
last_node.next_node = tail
return head
def get_size_of_linked_list(head_node:Node)->int:
size = 0
tmp_node = head_node
while tmp_node is not None:
tmp_node = tmp_node.next_node
size +=1
return size
# Example usage:
head_node = create_linked_list(10)
head_node.iterate_print_data()
[Head] -> [63] -> [46] -> [15] -> [17] -> [3] -> [9] -> [81] -> [44] -> [55] -> [94] -> [Tail]
Insert operation
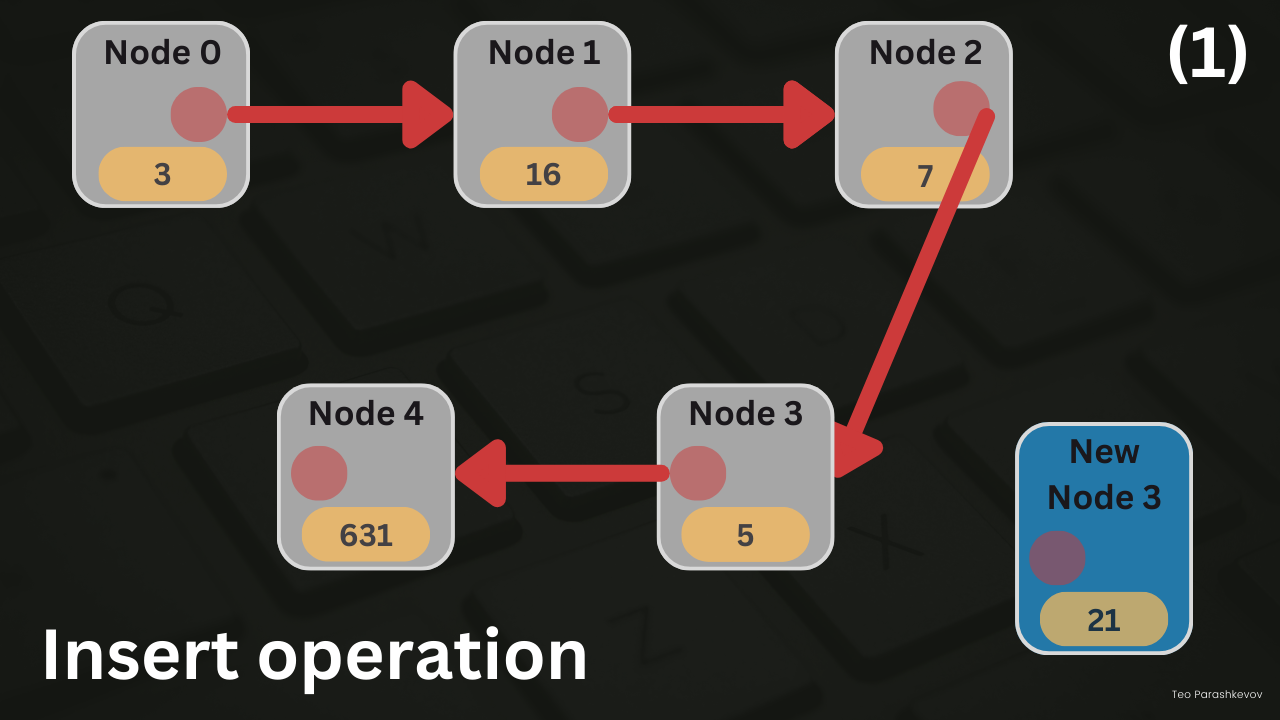
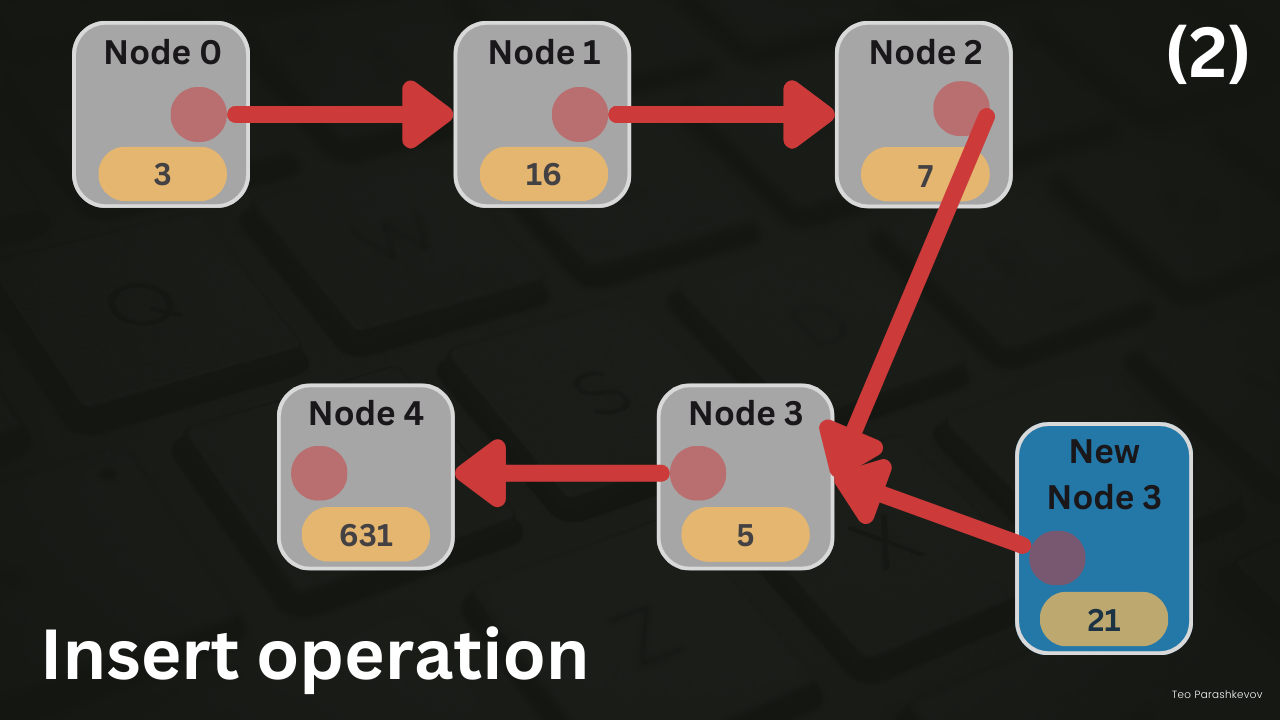
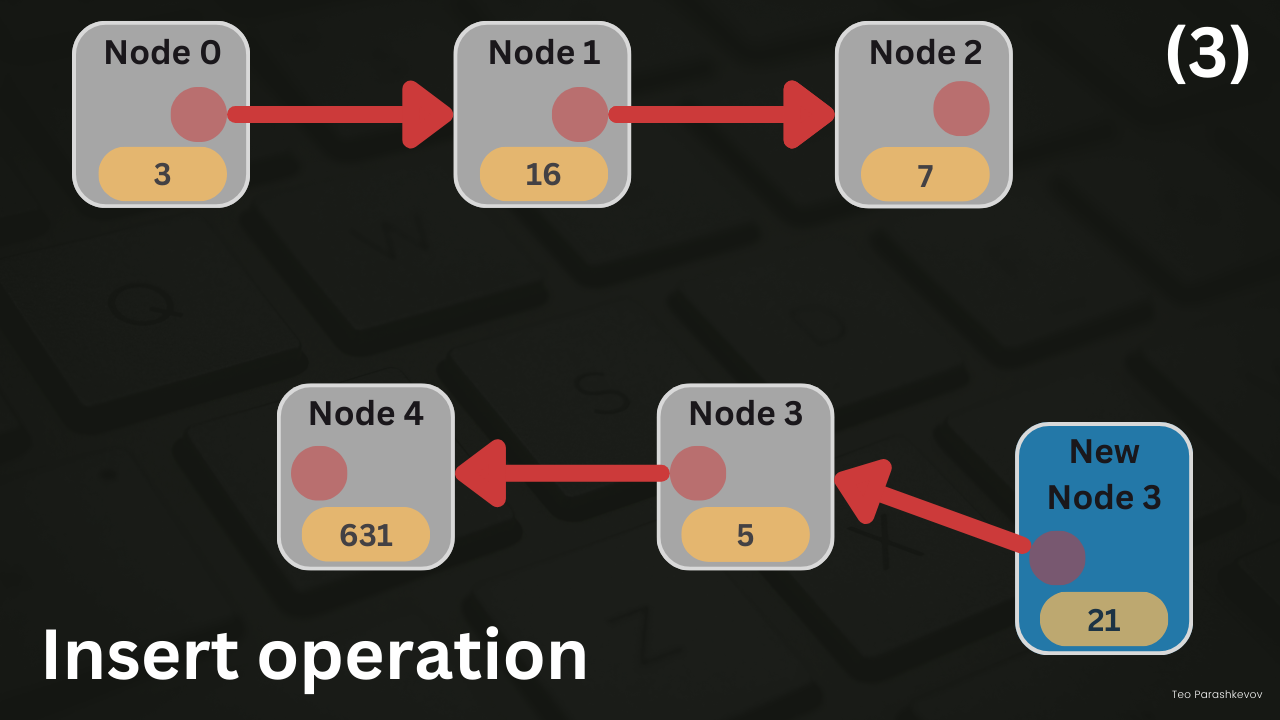
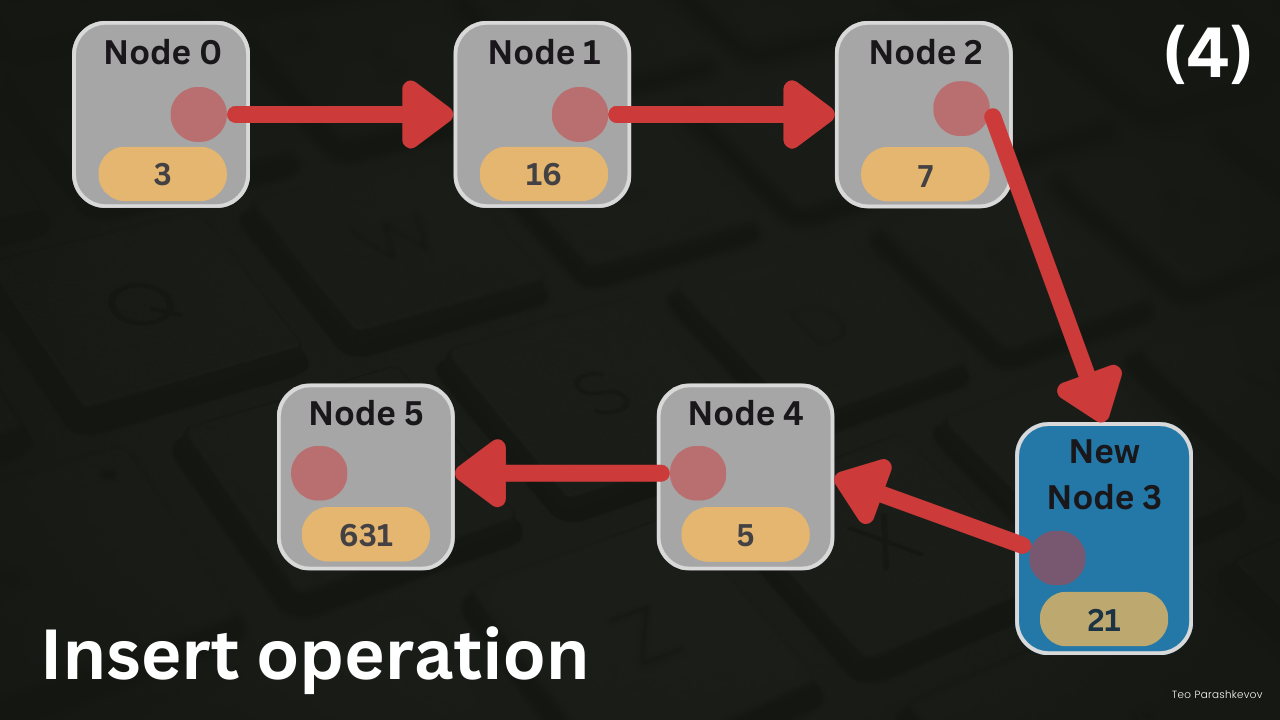
Insertion operation in a linked list can occur in three possible situations:
Insertion at the beginning (after the head node): In this situation, the new node is inserted right after the head node, becoming the new first node in the linked list. Steps for insertion at the beginning:
- Create a new node with the desired value.
- Set the next pointer of the new node to point to the node currently following the head node.
- Set the next pointer of the head node to point to the new node.
- Adjust the tail node pointer if necessary.
Insertion at the i-th position: In this situation, the new node is inserted at the ith position in the linked list, considering the head node as the first position. Steps for insertion at the ith position:
- Traverse the linked list, starting from the head node, to reach the (i-1)th node.
- Create a new node with the desired value.
- Set the next pointer of the new node to point to the node currently at the ith position.
- Set the next pointer of the (i-1)th node to point to the new node.
- Adjust the tail node pointer if necessary.
Insertion at the end (before the tail node): In this situation, the new node is inserted right before the tail node, becoming the new last node in the linked list. Steps for insertion at the end:
- Traverse the linked list, starting from the head node, until reaching the current tail node.
- Create a new node with the desired value.
- Set the next pointer of the new node to point to the current tail node.
- Set the next pointer of the previous node (predecessor of the tail node) to point to the new node.
- Update the tail node pointer to point to the new node.
Note: It’s important to handle boundary cases, such as empty lists or insertion beyond the current length of the linked list.
Insert at the beginning
- Create a new node with the desired value.
- Set the next pointer of the new node to point to the node currently following the head node.
- Set the next pointer of the head node to point to the new node.
- Adjust the tail node pointer if necessary.
# Create a random Linked List
head_node = create_linked_list(10)
print('Created Linked List')
head_node.iterate_print_data()
# Create new Node
new_node = Node(randint(1, 100))
print('The new node is ', new_node)
# Insert new_node at the beginning
new_node.next_node = head_node.next_node
head_node.next_node = new_node
# Print Linked List
head_node.iterate_print_data()
Created Linked List
[Head] -> [45] -> [59] -> [66] -> [33] -> [33] -> [1] -> [12] -> [79] -> [23] -> [30] -> [Tail]
The new node is [15]
[Head] -> [15] -> [45] -> [59] -> [66] -> [33] -> [33] -> [1] -> [12] -> [79] -> [23] -> [30] -> [Tail]
Insert at the i-th position
- Traverse the linked list, starting from the head node, to reach the (i-1)th node.
- Create a new node with the desired value.
- Set the next pointer of the new node to point to the node currently at the ith position.
- Set the next pointer of the (i-1)th node to point to the new node.
- Adjust the tail node pointer if necessary.
# Create a random Linked List
head_node = create_linked_list(10)
print('Created Linked List')
head_node.iterate_print_data()
# Create new Node
new_node = Node(randint(1, 100))
print('The new node is ', new_node)
# Insert new_node at the i-th position
i_th_position = 5
tmp_node = head_node
for i in range(i_th_position - 1):
tmp_node = tmp_node.next_node
new_node.next_node = tmp_node.next_node
tmp_node.next_node = new_node
# Print Linked List
print(f'Insert at {i_th_position}-th position')
head_node.iterate_print_data()
Created Linked List
[Head] -> [2] -> [46] -> [60] -> [41] -> [25] -> [27] -> [14] -> [67] -> [73] -> [73] -> [Tail]
The new node is [4]
Insert at 5-th position
[Head] -> [2] -> [46] -> [60] -> [41] -> [4] -> [25] -> [27] -> [14] -> [67] -> [73] -> [73] -> [Tail]
Insert at the end
- Traverse the linked list, starting from the head node, until reaching the current tail node.
- Create a new node with the desired value.
- Set the next pointer of the new node to point to the current tail node.
- Set the next pointer of the previous node (predecessor of the tail node) to point to the new node.
- Update the tail node pointer to point to the new node.
# Create a random Linked List
head_node = create_linked_list(10)
print('Created Linked List')
head_node.iterate_print_data()
# Create new Node
new_node = Node(randint(1, 100))
print('The new node is ', new_node)
# Insert new_node at the end position
tmp_node = head_node
tmp_next_node = tmp_node.next_node
while tmp_next_node.next_node is not None:
tmp_node = tmp_next_node
tmp_next_node = tmp_next_node.next_node
new_node.next_node = tmp_node.next_node
tmp_node.next_node = new_node
# Print Linked List
print(f'Insert at the end position')
head_node.iterate_print_data()
Created Linked List
[Head] -> [91] -> [1] -> [30] -> [10] -> [44] -> [79] -> [4] -> [79] -> [33] -> [14] -> [Tail]
The new node is [24]
Insert at the end position
[Head] -> [91] -> [1] -> [30] -> [10] -> [44] -> [79] -> [4] -> [79] -> [33] -> [14] -> [24] -> [Tail]
AVG Time
def insert_new_node(head_node:Node, idx:int):
if idx < 0:
return None
new_node = Node(randint(1, 100))
# print('The new node is ', new_node)
size_of_linked_list = get_size_of_linked_list(head_node)
# print(f'Size of Linked List: [{size_of_linked_list}]')
if idx == 0:
# Insert new_node at the beginning
new_node.next_node = head_node.next_node
head_node.next_node = new_node
elif idx < size_of_linked_list:
# Insert new_node at the i-th position
tmp_node = head_node
for i in range(idx - 1):
tmp_node = tmp_node.next_node
new_node.next_node = tmp_node.next_node
tmp_node.next_node = new_node
else:
# Insert new_node at the end position
tmp_node = head_node
tmp_next_node = tmp_node.next_node
while tmp_next_node.next_node is not None:
tmp_node = tmp_next_node
tmp_next_node = tmp_next_node.next_node
new_node.next_node = tmp_node.next_node
tmp_node.next_node = new_node
def time_insert(number_of_iterations:int = 1_000_000, position:str = 'beginning', print_output = False):
timed_results = []
size_of_linked_list = 1_000
for i in range(0, number_of_iterations):
print_percent = number_of_iterations / 10
if (i % print_percent == 0) and print_output:
print(f'[{i/10} %] ', end=' ')
# Create a linked list of random size [1, 1_000]
head:Node = create_linked_list(randint(1,size_of_linked_list))
if position == 'beginning':
idx = 0
elif position == 'middle':
idx = randint(1, size_of_linked_list - 1)
elif position == 'end':
idx = size_of_linked_list + 1
# Time [start]
start_time = time.time()
# Perform insert
insert_new_node(head, idx)
# Time [end]
end_time = time.time()
# Append to list
delta_t = end_time - start_time
timed_results.append(delta_t)
final_avg = sum(timed_results)/len(timed_results)
if print_output:
print('\nFinished Timing', end='\n')
print(final_avg)
return final_avg
bgn_avg_time = time_insert(number_of_iterations=1_000, position='beginning')
print('\n\n[Beginning]\n', bgn_avg_time)
middle_avg_time = time_insert(number_of_iterations=1_000, position='middle')
print('\n\n[i-th index],\n', middle_avg_time)
end_avg_time = time_insert(number_of_iterations=1_000, position='end')
print('\n\n[End]\n', end_avg_time)
[Beginning]
3.9842844009399414e-05
[i-th index],
5.733442306518555e-05
[End]
7.230186462402343e-05
Delete operation
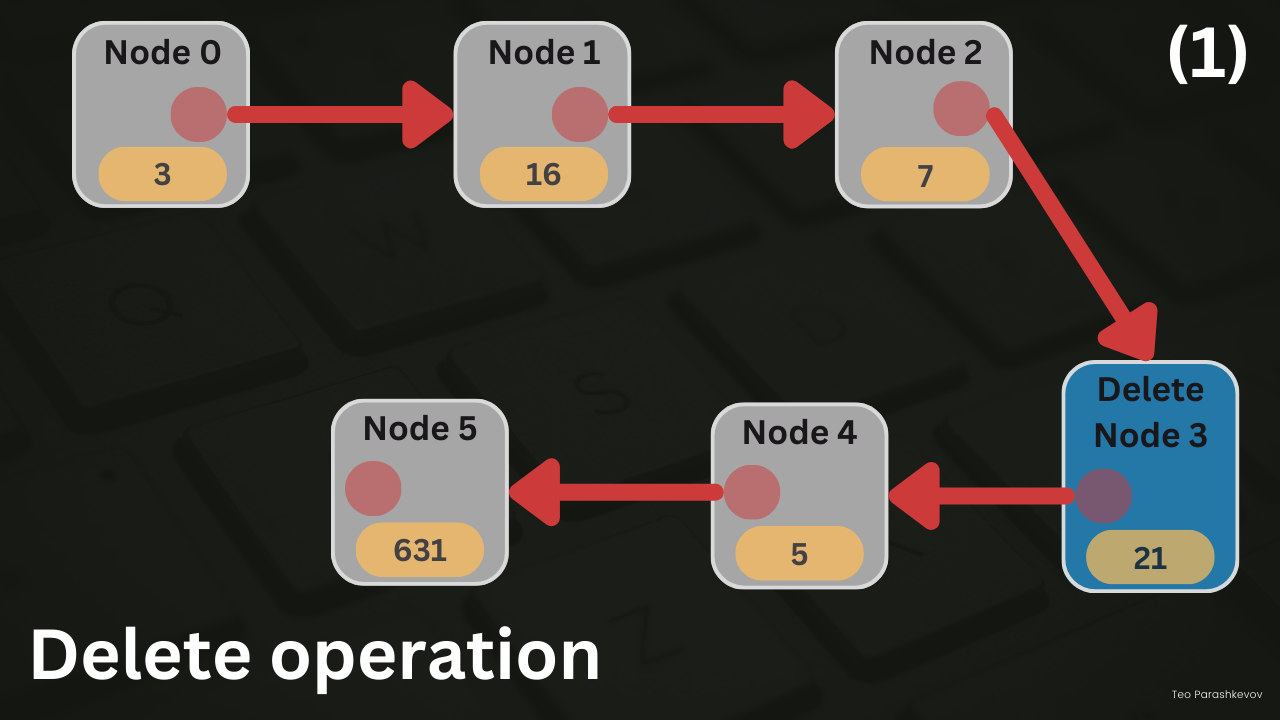
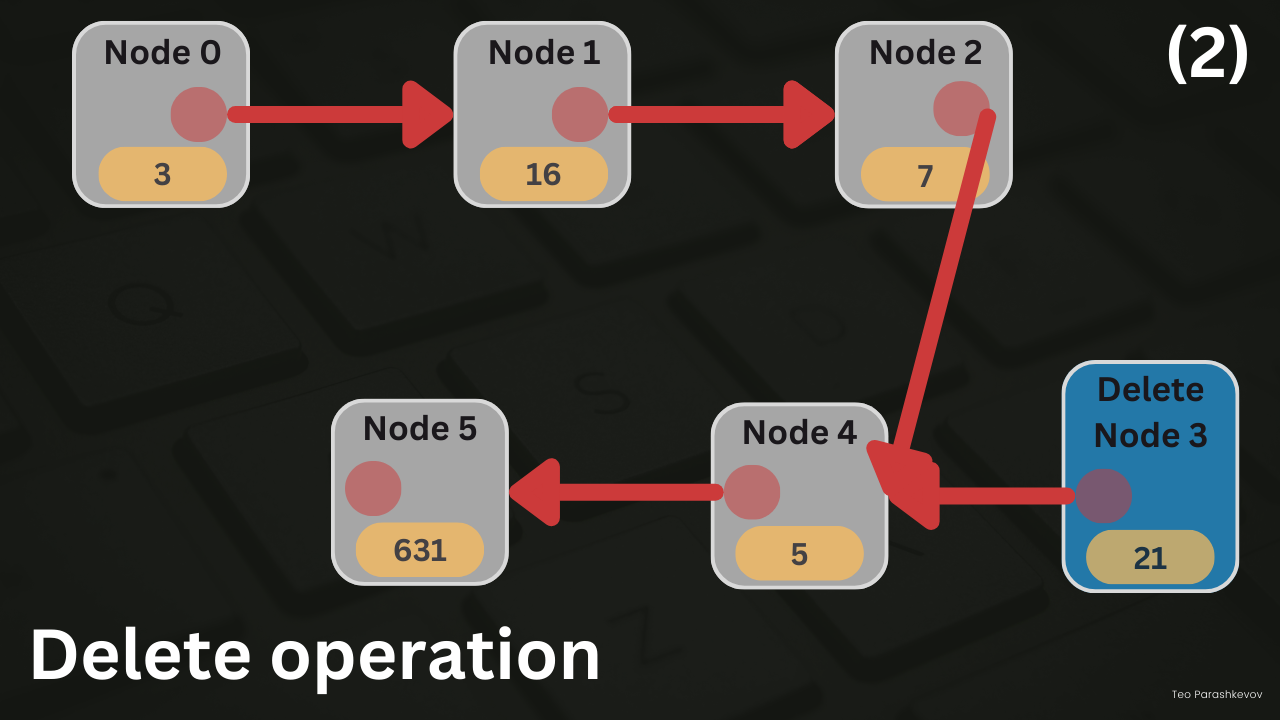
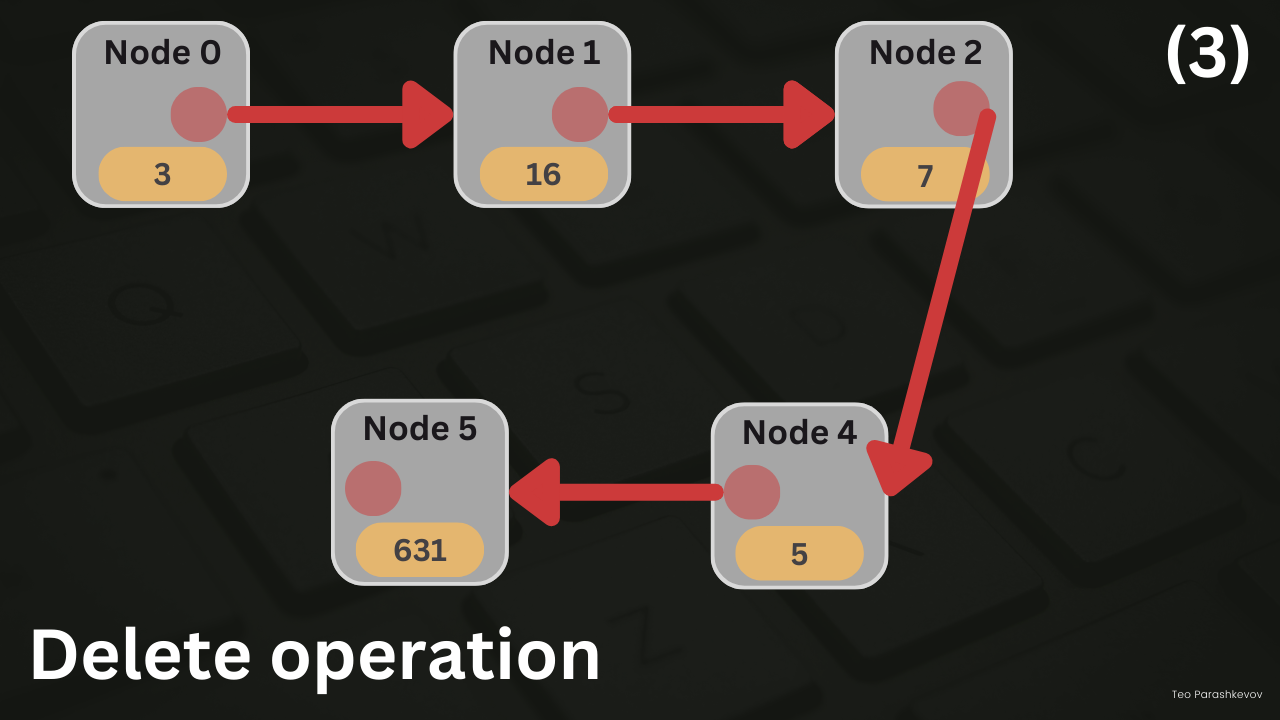
Deletion operation in a linked list can occur in three possible situations:
Deleting the first node: In this situation, we simply update the head pointer to skip the first node, effectively removing it from the linked list. Then, we proceed to free the memory allocated for the first node to prevent memory leaks.
- Set the head of the linked list to the next node.
- Free the memory of the node that was initially the first node.
Deleting the i-th node: To delete the ith node, we first traverse the linked list to reach the (i-1)th node. Then, we update its next pointer to skip the ith node and directly point to the (i+1)th node, bypassing the node we want to delete. Finally, we free the memory allocated for the ith node.
- Traverse the linked list to find the (i-1)th node.
- Update the next pointer of the (i-1)th node to skip the ith node and point to the (i+1)th node.
- Free the memory of the ith node.
Deleting the last node: In this situation, we need to traverse the linked list until we reach the second-to-last node. Then, we update its next pointer to NULL, effectively removing any reference to the last node. Finally, we free the memory allocated for the last node to prevent memory leaks.
- Traverse the linked list to find the second-to-last node (i.e., the (n-1)th node, where n is the total number of nodes).
- Update the next pointer of the second-to-last node to point to NULL.
- Free the memory of the last node.
These steps and descriptions illustrate the operations involved in deleting a node from a linked list in different scenarios.
Delete the first node
- Set the head of the linked list to the next node.
- Free the memory of the node that was initially the first node.
# Create a random Linked List
head_node = create_linked_list(10)
print('Created Linked List')
head_node.iterate_print_data()
# Delete the 1st node
tmp_node = head_node.next_node
head_node.next_node = tmp_node.next_node
print(f'Deleting {tmp_node}')
del tmp_node
# Print Linked List
head_node.iterate_print_data()
Created Linked List
[Head] -> [85] -> [13] -> [37] -> [13] -> [21] -> [83] -> [25] -> [77] -> [53] -> [55] -> [Tail]
Deleting [85]
[Head] -> [13] -> [37] -> [13] -> [21] -> [83] -> [25] -> [77] -> [53] -> [55] -> [Tail]
Delete the i-th node
- Traverse the linked list to find the (i-1)th node.
- Update the next pointer of the (i-1)th node to skip the ith node and point to the (i+1)th node.
- Free the memory of the ith node.
# Create a random Linked List
head_node = create_linked_list(10)
print('Created Linked List')
head_node.iterate_print_data()
# Delete the i-th node
i_th_position = 5
tmp_node = head_node.next_node
prev_node = None
for i in range(i_th_position - 1):
prev_node = tmp_node
tmp_node = tmp_node.next_node
prev_node.next_node = tmp_node.next_node
print(f'Deleting {tmp_node}')
del tmp_node
# Print Linked List
head_node.iterate_print_data()
Created Linked List
[Head] -> [2] -> [92] -> [53] -> [52] -> [36] -> [10] -> [96] -> [51] -> [92] -> [3] -> [Tail]
Deleting [36]
[Head] -> [2] -> [92] -> [53] -> [52] -> [10] -> [96] -> [51] -> [92] -> [3] -> [Tail]
Delete the last node
- Traverse the linked list to find the second-to-last node (i.e., the (n-1)th node, where n is the total number of nodes).
- Update the next pointer of the second-to-last node to point to NULL.
- Free the memory of the last node.
# Create a random Linked List
head_node = create_linked_list(10)
print('Created Linked List')
head_node.iterate_print_data()
# Delete the i-th node
tmp_node = head_node.next_node
prev_node = None
while tmp_node.next_node.next_node is not None:
prev_node = tmp_node
tmp_node = tmp_node.next_node
prev_node.next_node = tmp_node.next_node
print(f'Deleting {tmp_node}')
del tmp_node
# Print Linked List
head_node.iterate_print_data()
Created Linked List
[Head] -> [39] -> [50] -> [30] -> [9] -> [71] -> [19] -> [66] -> [46] -> [8] -> [93] -> [Tail]
Deleting [93]
[Head] -> [39] -> [50] -> [30] -> [9] -> [71] -> [19] -> [66] -> [46] -> [8] -> [Tail]
def delete_node(head_node:Node, idx:int):
if idx < 0:
return None
size_of_linked_list = get_size_of_linked_list(head_node)
# print(f'Size of Linked List: [{size_of_linked_list}]')
if idx == 0:
# Delete node from beginning
tmp_node = head_node.next_node
head_node.next_node = tmp_node.next_node
del tmp_node
elif idx < size_of_linked_list:
# Delete node from the i-th position
tmp_node = head_node.next_node
prev_node = tmp_node
for i in range(idx - 1):
prev_node = tmp_node
tmp_node = tmp_node.next_node
prev_node.next_node = tmp_node.next_node
del tmp_node
else:
# Delete node from end
tmp_node = head_node.next_node
prev_node = tmp_node
while tmp_node.next_node.next_node is not None:
prev_node = tmp_node
tmp_node = tmp_node.next_node
prev_node.next_node = tmp_node.next_node
del tmp_node
def time_delete(number_of_iterations:int = 1_000_000, position:str = 'beginning', print_output = False):
timed_results = []
size_of_linked_list = 1_000
for i in range(0, number_of_iterations):
print_percent = number_of_iterations / 10
if (i % print_percent == 0) and print_output:
print(f'[{i/10} %] ', end=' ')
# Create a linked list of random size [1, 1_000]
head:Node = create_linked_list(randint(1,size_of_linked_list))
if position == 'beginning':
idx = 0
elif position == 'middle':
idx = randint(1, size_of_linked_list - 1 )
elif position == 'end':
idx = size_of_linked_list + 1
# Time [start]
start_time = time.time()
# Perform insert
delete_node(head, idx)
# Time [end]
end_time = time.time()
# Append to list
delta_t = end_time - start_time
timed_results.append(delta_t)
final_avg = sum(timed_results)/len(timed_results)
if print_output:
print('\nFinished Timing', end='\n')
print(final_avg)
return final_avg
bgn_avg_time = time_delete(number_of_iterations=1_000, position='beginning')
print('\n\n[Beginning]\n', bgn_avg_time)
middle_avg_time = time_delete(number_of_iterations=1_000, position='middle')
print('\n\n[i-th index],\n', middle_avg_time)
end_avg_time = time_delete(number_of_iterations=1_000, position='end')
print('\n\n[End]\n', end_avg_time)
[Beginning]
3.8056135177612305e-05
[i-th index],
6.313323974609375e-05
[End]
7.75747299194336e-05
insert_time_dictionary = {
'iterations':[],
'beginning': [],
'middle': [],
'end':[]
}
for iterations in range(10, 1_000_000, 10):
if iterations % 1_000 == 0:
print('.', end=' ')
bgn_avg_t = time_insert(number_of_iterations=iterations, position='beginning')
mdl_avg_t = time_insert(number_of_iterations=iterations, position='middle')
end_avg_t = time_insert(number_of_iterations=iterations, position='end')
insert_time_dictionary['iterations'].append(iterations)
insert_time_dictionary['beginning'].append(bgn_avg_t)
insert_time_dictionary['middle'].append(mdl_avg_t)
insert_time_dictionary['end'].append(end_avg_t)
insert_operation_df = pd.DataFrame(insert_time_dictionary)
insert_operation_df.head(10)
insert_operation_df.to_csv('insert_operation_timed.csv')
Applications
Expression parser
# Declare Nodes
expression_head = Node('Head')
expression_tail = Node('Tail')
e_node_1 = Node((2, 0)) # 2
e_node_2 = Node((5, 1)) # 5x
e_node_3 = Node((13, 2)) # 13x^2
e_node_4 = Node((97, 3)) # 97x^3
e_node_5 = Node((8, 4)) # 8x^4
e_node_6 = Node((23, 5)) # 23x^5
# Assign pointers
expression_head.next_node = e_node_1
e_node_1.next_node = e_node_2
e_node_2.next_node = e_node_3
e_node_3.next_node = e_node_4
e_node_4.next_node = e_node_5
e_node_5.next_node = e_node_6
e_node_6.next_node = expression_tail
# Print expression
expression_head.iterate_print_data()
[Head] -> [(2, 0)] -> [(5, 1)] -> [(13, 2)] -> [(97, 3)] -> [(8, 4)] -> [(23, 5)] -> [Tail]
Expression Addition
def expression_create_linked_list(size_of_list, size_of_coef, size_of_exp):
if size_of_exp <= size_of_list:
raise Exception('(size_of_exp) must be greater than (size_of_list)')
expression_head = Node('Head')
expression_tail = Node('Tail')
tmp_exponent = 1
last_exponent = tmp_exponent
for i in range(0, size_of_list):
_exp_upper_limit = (i+1)*int(size_of_exp/size_of_list)
# Create coeficient and exponent
_coef = randint(1, size_of_coef)
_exp = randint(tmp_exponent+1, _exp_upper_limit)
_node = Node((_coef, _exp))
# Assign Node
if expression_head.next_node is None:
expression_head.next_node = _node
else:
tmp_node = expression_head.next_node
while tmp_node.next_node is not None:
tmp_node = tmp_node.next_node
tmp_node.next_node = _node
tmp_exponent = _exp
# Assign Tail
tmp_node = expression_head.next_node
while tmp_node.next_node is not None:
tmp_node = tmp_node.next_node
tmp_node.next_node = expression_tail
return expression_head
def expression_add_two_expressions(expression_1, expression_2):
sum_expression_head = Node('Head')
sum_expression_last_node = sum_expression_head
sum_expression_tail = Node('Tail')
tmp_node_exp_1 = expression_1.next_node if 'Head' in str(expression_1) else expression_1
tmp_node_exp_2 = expression_2.next_node if 'Head' in str(expression_2) else expression_2
while (tmp_node_exp_1 is not None) and (tmp_node_exp_2 is not None):
if ('Tail' in str(tmp_node_exp_1)) and ('Tail' in str(tmp_node_exp_2)):
break
#
if ('Tail' in str(tmp_node_exp_1)) or (tmp_node_exp_1 is None):
# add current expression_2
_tmp_node = deepcopy(tmp_node_exp_2)
_tmp_node.next_node = None
sum_expression_last_node.next_node = _tmp_node
sum_expression_last_node = sum_expression_last_node.next_node
# move expression_2
tmp_node_exp_2 = tmp_node_exp_2.next_node
continue
#
if ('Tail' in str(tmp_node_exp_2)) or (tmp_node_exp_2 is None):
# add current expression_1
_tmp_node = deepcopy(tmp_node_exp_1)
_tmp_node.next_node = None
sum_expression_last_node.next_node = _tmp_node
sum_expression_last_node = sum_expression_last_node.next_node
# move expression_1
tmp_node_exp_1 = tmp_node_exp_1.next_node
continue
_coef_1 = tmp_node_exp_1.data[0]
_exp_1 = tmp_node_exp_1.data[1]
_coef_2 = tmp_node_exp_2.data[0]
_exp_2 = tmp_node_exp_2.data[1]
if _exp_1 == _exp_2:
# print('Adding: ', tmp_node_exp_1, tmp_node_exp_2)
# create new node
_data = (_coef_1+_coef_2, _exp_1)
tmp_sum_expression_node = Node(_data)
tmp_sum_expression_node.next_node = None
# add to sum_expression
sum_expression_last_node.next_node = tmp_sum_expression_node
sum_expression_last_node = sum_expression_last_node.next_node
# move expression_1 and expression_2
tmp_node_exp_1 = tmp_node_exp_1.next_node
tmp_node_exp_2 = tmp_node_exp_2.next_node
continue
elif _exp_1 < _exp_2:
# print(tmp_node_exp_2, f' has an exponent of {_exp_2}, which is greater than {_exp_1}', tmp_node_exp_1)
# add current expression_1
_tmp_node = deepcopy(tmp_node_exp_1)
_tmp_node.next_node = None
sum_expression_last_node.next_node = _tmp_node
sum_expression_last_node = sum_expression_last_node.next_node
# move expression_1
tmp_node_exp_1 = tmp_node_exp_1.next_node
continue
elif _exp_1 > _exp_2:
# print(tmp_node_exp_1, f' has an exponent of {_exp_1}, which is greater than {_exp_2}', tmp_node_exp_2)
# add current expression_2
_tmp_node = deepcopy(tmp_node_exp_2)
_tmp_node.next_node = None
sum_expression_last_node.next_node = _tmp_node
sum_expression_last_node = sum_expression_last_node.next_node
# move expression_2
tmp_node_exp_2 = tmp_node_exp_2.next_node
continue
else:
pass
sum_expression_last_node.next_node = sum_expression_tail
return sum_expression_head
expression_head_1 = expression_create_linked_list(5, 10, 10)
expression_head_2 = expression_create_linked_list(5, 10, 10)
expression_head_1.iterate_print_data()
print()
expression_head_2.iterate_print_data()
print()
sum_of_expressions_head = expression_add_two_expressions(expression_head_1, expression_head_2)
sum_of_expressions_head.iterate_print_data()
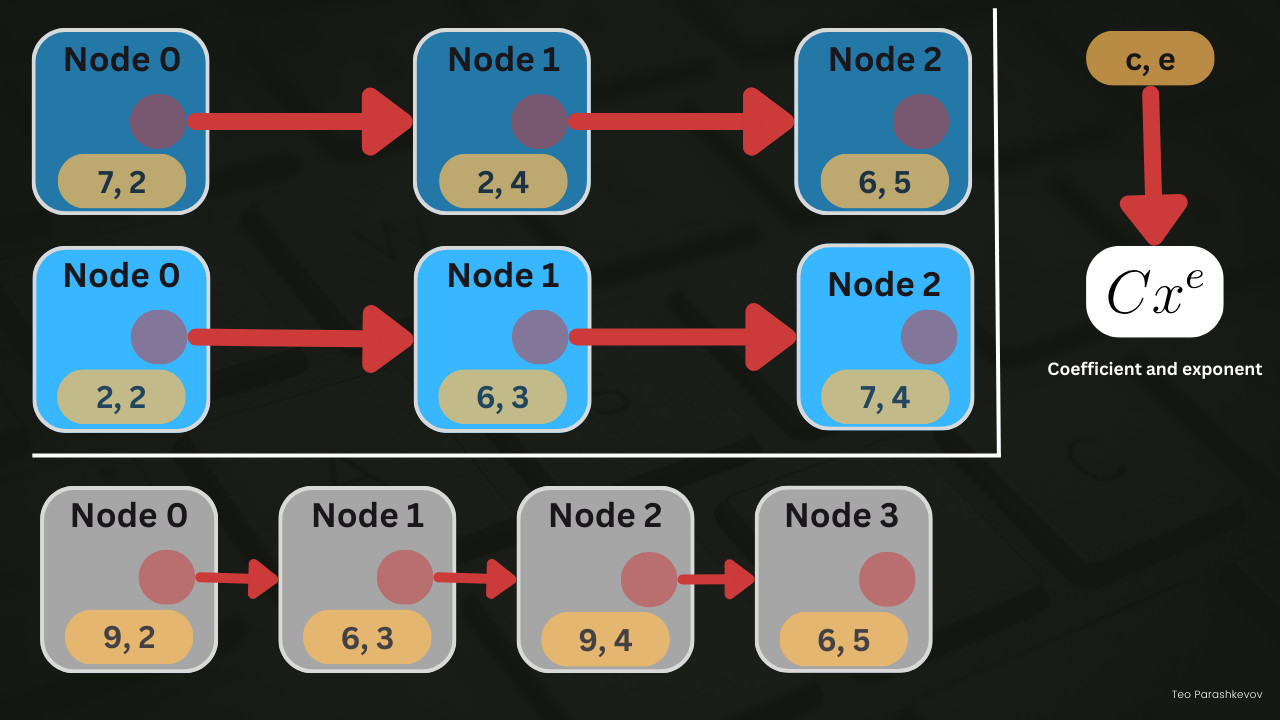
[Head] -> [(7, 2)] -> [(2, 4)] -> [(6, 5)] -> [(10, 8)] -> [(4, 10)] -> [Tail]
[Head] -> [(2, 2)] -> [(6, 3)] -> [(7, 4)] -> [(7, 7)] -> [(9, 10)] -> [Tail]
[Head] -> [(9, 2)] -> [(6, 3)] -> [(9, 4)] -> [(6, 5)] -> [(7, 7)] -> [(10, 8)] -> [(13, 10)] -> [Tail]